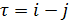Кодирование с линейным предсказанием (LPC — Linear Predictive Coding). Рекомендации G.728, G.729, G.723
При кодировании с линейным предсказанием моделируются различные параметры человеческой речи, которые передаются вместо отсчетов или их разности, требующих значительно большей пропускной способности канала. Следует заметить, что буферы, необходимые для хранения потоков данных, увеличивают задержку кодирования.
Первые реализации LPC, такие как LPC-вокодер, были предназначены ля передачи данных на низких скоростях – 2,4 и 4,8 кбит/с. На скорости 2,4 кбит/с обеспечивался приемлемый уровень разборчивости речи, однако качество, естественность и узнаваемость речи недостаточны. Поскольку этот метод сильно зависит от точного воспроизведения человеческой речи, его реализации, такие как LPC-вокодер, не подходят для сигналов неречевого происхождения, например сигналов модема.
Широко используемый в настоящее время метод кодирования с линейным предсказанием работает с блоками отсчетов, для каждого из которых вычисляется и передается частота основного тона, его амплитуда и информация о типе возбуждающего воздействия.
Структура синтезатора речи с линейным предсказанием показана на рис. 2.5. Здесь управляющий вход или сигнал возбуждения смоделирован в виде последовательности импульсов на частоте основного тона (для вокализованной речи) или случайный шум (для невокализированной речи).
Комбинированные спектральные составляющие потока от голосовых связок, голосового тракта и звукообразования за счет губ могут быть представлены цифровым фильтром с изменяющимися параметрами и передаточной функцией
(2.7)
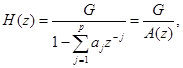
где 
Параметрами, характеризующими голосовой тракт, являются коэффициенты знаменателя и масштабный множитель G.
Преобразуя уравнение (2.7) во временную область, можно получить разностное уравнение для импульсной характеристики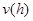 
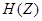
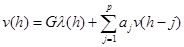
, соответствующей 
:
(2.8)
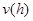
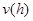
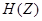
Уравнение (2.8) называют разностным уравнением LPC. Оно устанавливает, что текущее значение выходного сигнала может быть определено суммированием взвешенного текущего входного значения и взвешенной суммы предыдущих выходных выборок. Следовательно, в LPC анализе проблема может быть сформулирована так: даны измерения сигнала , требуется определить параметры передаточной функции системы 
.
Линейное предсказание при анализе речевых сигналов обычно используется в двух направлениях. Одно из них – проведение кратковременного спектрального анализа речи. Второе направление – построение систем анализа-синтеза.
Параметры, входящие в функцию предсказания, через формулу (2.7) определяют параметры передаточной функции голосового тракта. Может быть предложено несколько вариантов структуры анализатора, пригодных для построения синтезатора и реализующих передаточную функцию голосового тракта. Структуру прямой формы можно получить непосредственно по коэффициентам функции предсказания. С другой стороны, дробь (2.7) можно преобразовать в произведение и получить структуру каскадной формы.
Во всех случаях параметры синтезатора непрерывно обновляются при смене анализируемых кадров речи. Чтобы избежать эффектов, связанных со скачками значений параметров, необходимо плавно изменять параметры с помощью интерполяции при переходе от одного участка речи к другому. При прямой форме синтеза может возникать ситуация, соответствующая неустойчивому фильтру, хотя исходные значения относились к устойчивому фильтру. В каскадной структуре устойчивость обеспечивается проще.Определение параметров возбуждающего сигнала в системе анализа-синтеза с линейным предсказанием, как правило, основывается на исследовании сигнала ошибки, получаемого пропусканием исходного речевого сигнала через фильтр с характеристикой, обратной той характеристике, которая аппроксимирует передаточную функцию голосового тракта. Полученный сигнал ошибки является аппроксимацией сигнала, возбуждающего речевое колебание. Для определения параметров возбуждающего сигнала можно применить один из известных алгоритмов различения звонкой и глухой речи, а также оценки периода основного тона, например на основе рассмотренного выше корреляционного анализа сигналов во временной области.
Источник
Русские Блоги
Адаптивная фильтрация-линейное предсказание (LPC)
Время: 2017-03-26 10:12:07
【Заметки для чтения 05】
Предисловие
В главе 3 четвертого издания Саймона Хекина «Принципы адаптивных фильтров» линейное предсказание — это применение фильтра Винера как функции распознавания сигналов и способа реализации кодирования сигналов. Я думал о том, чтобы пропустить эту главу, но я думал о записи каждой главы, пока не увидел Фильтр Калмана, просто запишите его. в основном включают:
1) Принцип прямого линейного предсказания;
2) Примеры приложений линейного прогнозирования;
Это ваши собственные заметки для изучения. Если есть какие-либо несоответствия, я надеюсь, вы поможете мне указать на них!
1. Принцип прямого линейного прогнозирования
Взяв в качестве примера голосовые сигналы, можно представить себе модель речевого тракта: формантную модель каскадной структуры. То есть: для общих гласных можно использовать многополюсную модель, а передаточную функцию:
G — коэффициент амплитуды, p — количество полюсов.
Здесь обсуждается только всеполюсная модель. Для выхода $ x (n) $ и возбуждения $ u (n) $ существуют разностные уравнения:
$x\left( n \right) = \sum\limits_^p <
$\hat x\left( n \right) = \sum\limits_^p <
Это линейный предсказатель. $ \ hat x \ left (n \ right) $ — это оценочное значение $ x (n) $. $ a_i $ — коэффициент прогнозирования (коэффициент линейного прогнозирования, LPC), а $ p $ — соответствующий порядок.
Соответствующая ошибка одноточечного прогноза:
$e(n) = x(n) — \hat x\left( n \right) = x(n) — \sum\limits_^p <
Частную производную $ a_i $ можно решить, и полученные уравнения обычно называют уравнениями Юла-Уокера.
Два, примеры применения
Используйте коэффициент прогнозирования для оценки приблизительного отклика системы $ H $. Коэффициент может использоваться для характеристики характеристик речи, или приближенный $ H $ может использоваться для наблюдения за характеристиками речевого тракта, а также может выполняться извлечение формант. Это можно рассматривать как характеристики говорящего.
Соответствующий график результатов:
Можно видеть, что частотный спектр сигнала модулирует высокочастотный сигнал медленно меняющейся составляющей, и соответствующая временная область является сверткой, а модель канала соответствует $ h (n) $ свертки. Если p выбрано слишком маленьким, а оценка неточна, легко выбрать слишком большой Чрезмерная подгонка, поэтому кажется, что LPC — это предсказание, а на самом деле проблема подгонки. Существует также чрезмерная подгонка. После получения спектра LPC вы можете использовать поиск пиков и другие методы для оценки форманты.
Источник
Глава 2. Построение метода сжатия речевых сигналов
Описание алгоритмов сжатия речевых сигналов
Алгоритм LPC(линейное предсказание)
Рассмотрим следующую модель речеобразования (рис. 3): система возбуждается импульсной последовательностью для вокализованных звуков речи и шумом для невокализованных [5]. Данная модель имеет следующие параметры: классификатор вокализованных и невокализованных звуков, период основного тона для вокализованных звуков, коэффициент усиления 
и коэффициенты 
цифрового фильтра. Данные параметры медленно меняются с течением времени. Здесь задача определения коэффициентов цифрового фильтра является наиболее значимой.
Рис.3. Структурная схема упрощённой модели речеобразования
Алгоритм линейного предсказания основан на предположении о том, что отсчёты сигнала 
связаны с сигналами возбуждения 
линейным разностным уравнением [5, 6]
. (1)
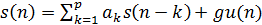
Тогда передаточная функция линейной системы с входом и выходом имеет вид:
, (2)
где 
– формальная переменная, 
и 
– z-преобразования речевого сигнала и сигнала возбуждения .
Определим линейный предсказатель с коэффициентами 
как систему, на выходе которой в момент времени n имеем
. (3)
Системной функцией предсказателя p-го порядка является полином вида
. (4)
Погрешность предсказания будет иметь вид
. (5)
Иными словами, мы имеем следующую передаточную функцию:
. (6)
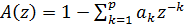
Тогда погрешность предсказания будет представлять собой сигнал на выходе системы с данной передаточной функцией.
Для данной модели выполнено равенство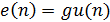 
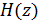
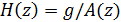
. Следовательно, фильтр погрешности предсказания 
является обратным фильтром к системе с передаточной функцией 
. Таким образом, мы приходим к следующему равенству:
. (7)
Основной задачей анализа на основе использования инструмента линейного предсказания является определение параметров ,k=1, 2, …, p, где p – порядок анализа [6]. Эти параметры определяются по речевому сигналу.Предполагается, что данные параметры являются параметрами функции в модели речеобразования. В силу изменения свойств речевого сигнала во времени параметры предсказания (их также называют коэффициентами предсказания) должны оцениваться на коротких сегментах речи, называемых кадрами.В качестве критерия оценки берётся минимум суммы квадратов погрешностей линейного предсказания на сегменте речевого сигнала. По данному критерию производится оптимизация синтеза фильтра .
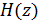
Пусть задан некоторый отрезок [n0; n1]. Тогда сумма квадратов погрешностей линейного предсказания определяется так:
. (8)
Тогда коэффициенты линейного предсказания можно получить, минимизируя 
. В итоге получим систему p линейных уравнений относительно p неизвестных a1, a2, …, ap:
, j=1, 2, …, p, (9)
. (10)
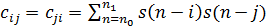
Полученная система носит название системы Юла-Уокера. Решив эту систему, несложно оценить и минимальную достижимую погрешность предсказания.
Проделав некоторые преобразования, получим
. (11)
Для определения коэффициентов линейного предсказания из системы уравнений Юла-Уокера нужно найти величины 
, i=0, 1, …, p, j=1, 2, …, p, где p– порядок линейного предсказания.
Существует множество подходов к вычислению этих величин, включая метод ковариации, метод автокорреляции, метод решётки и т. д. При реализации данного алгоритма было решено воспользоваться методом автокорреляции.
В данном методе пределы анализа полагаются равными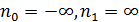 
. Сигнал вне интервала обнуляется, т. е. 
при 
.Взятие таких пределов позволяет упростить выражение для , i=1, 2, …, p, j=0, 1, …, p.
. (12)
– функции величины 
, с точностью до множителя совпадающие с оценками автокорреляционной функции 
сигнала , вычисленными при 
. (13)
Поделим уравнения в системе (9) наN. В результате получим систему уравнений Юла-Уокера для автокорреляционного метода:
, j=1, 2, …, p. (14)
Данная система может быть записана в матричном виде как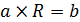 
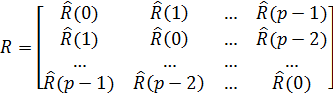
, где
. (15)
Стоит отметить, что матрица Rв таком методе обладает важными свойствами: она симметрическая и теплициева. Такая структура матрицы позволяет решить систему (14) особенно просто: решение находится за 
операций по алгоритму Левинсона-Дарбина[7].
Анализ на основе линейного предсказания также называют LP-анализом (или LPC-анализом).
Ниже приведена блок-схема устройства LPC-10 вокодера (рис. 4), описывающая общую схему его работы. Порядок LPC-анализа равен 10.
Рис.4. Блок-схема устройства LPC-10 вокодера
Скорость вокодера LPC-10 составляет 2400 kbps. ПорядокLPC-анализа pдля данного вокодера равен 10, т. е. на каждом сегменте берётся 10 коэффициентов предсказания. Длина каждого кадра (сегмента) равна 20 мс. Таким образом, скорость составляет 50 кадров в секунду. В сумме на каждый кадр отводится 48 бит.Следует отметить, что помимо распределения битов, указанного непосредственно в стандарте LPC-10E [17], существуют и другие варианты распределения битов. Например, в одном из таких вариантов эти биты распределены следующим образом [8]:
Кодирование параметров LPC-10 вокодера в битах.
| Название параметра | Нотация параметра | Число бит на кадр | |||||||||||||||||||||||||||||||||||||||||||||
| Коэффициенты линейного предсказания | 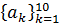 | 34 | |||||||||||||||||||||||||||||||||||||||||||||
| Коэффициент усиления | G | 7 | |||||||||||||||||||||||||||||||||||||||||||||
| Период основного тона | V/UV, T | 7 | |||||||||||||||||||||||||||||||||||||||||||||
| LPC | Число бит |
 | 3 |
 | 4 |
 | 4 |
 | 4 |
 | 4 |
 | 3 |
 | 3 |
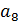 | 3 |
 | 3 |
 | 3 |
| Итого | 34 |
Значение коэффициента усиления Gкодируется 7 битами.
Для вокализованной речи значения T варьируются в диапазоне от 20 до 146. V/UV, T вместе кодируются следующим образом:
Кодирование значения высоты тона.
| V/UV | T | Кодированное значение |
| UV | — | 0 |
| V | 20 | 1 |
| V | 21 | 2 |
| V | 22 | 3 |
| V | 23 | 4 |
| … | … | … |
| V | 146 | 127 |
Таким образом, данное значение можно закодировать 7 битами.
Дата добавления: 2018-06-27 ; просмотров: 447 ; Мы поможем в написании вашей работы!
Источник
