Roc auc константное предсказание

Глубокое погружение в ROC-AUC

Я думаю, что большинство людей слышали о ROC-кривой или о AUC (площади под кривой) раньше. Особенно те, кто интересуется наукой о данных. Однако, что такое ROC-кривая и почему площадь под этой кривой является хорошей метрикой для оценки модели классификации?

Теория ROC-кривой

Полное название ROC — Receiver Operating Characteristic (рабочая характеристика приёмника). Впервые она была создана для использования радиолокационного обнаружения сигналов во время Второй мировой войны. США использовали ROC для повышения точности обнаружения японских самолетов с помощью радара. Поэтому ее называют рабочей характеристикой приемника.

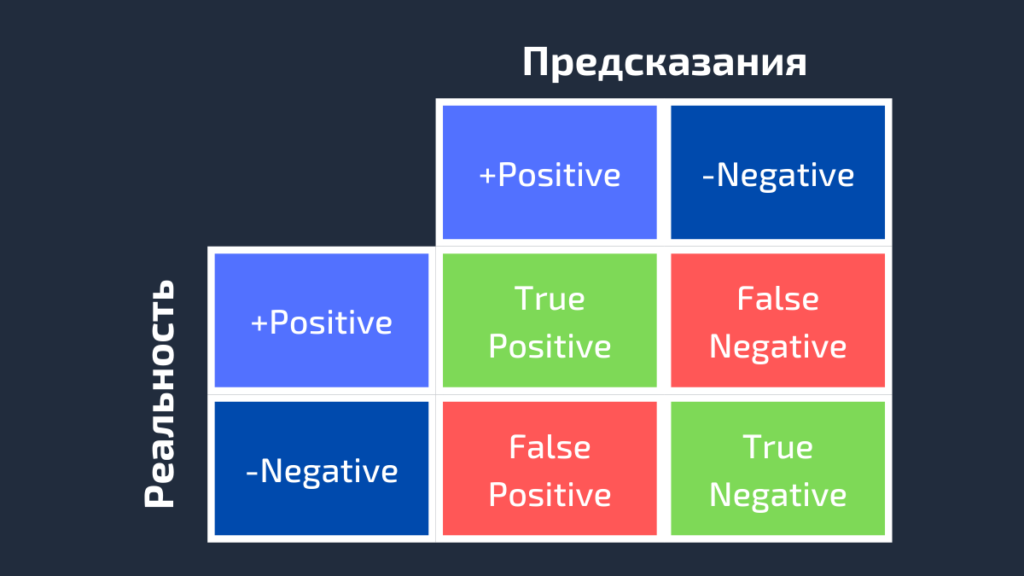
AUC или area under curve — это просто площадь под кривой ROC. Прежде чем мы перейдем к тому, что такое ROC-кривая, нужно вспомнить, что такое матрица ошибок.

Как видно из рисунка выше, матрица ошибок — это комбинация вашего прогноза (1 или 0) и фактического значения (1 или 0). В зависимости от результата предсказания и того, корректна ли была проведена классификация, матрица разделена на 4 части. Например, true positive (истинно положительный) результат — это количество случаев, в которых вы правильно классифицируете семпл как положительный. А false positive (ложноположительный) — это число случаев, в которых вы ошибочно классифицируете семпл как положительный.

Матрица ошибок содержит только абсолютные числа. Однако, используя их, мы можем получить множество других метрик, основанных на процентных соотношениях. True Positive Rate (TPR) и False Positive Rate (FPR) — две из них.

True Positive Rate (TPR) показывает, какой процент среди всех positive верно предсказан моделью.
TPR = TP / (TP + FN).

False Positive Rate (FPR): какой процент среди всех negative неверно предсказан моделью.
FPR = FP / (FP + TN).

Хорошо, давайте теперь перейдем к кривой ROC!

Что такое ROC-кривая?

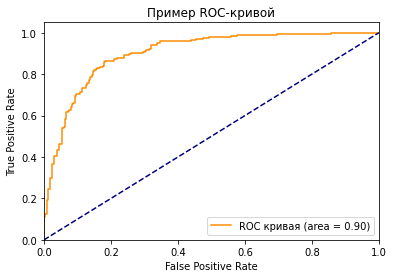
Как вы можете видеть на графике, кривая ROC — это просто отношение TPR к FPR. Теперь вам все понятно, в заключение…

Поверили?
Если серьезно, вы можете прочитать намного больше информации из диаграммы. Первый вопрос, который я хочу здесь обсудить: у нас же есть только один набор TPR, FPR, посчитанный на основе сделанных моделью предсказаний. Так откуда взялось такое количество точек для построения целого графика?

Все следует из того, как работает модель классификации. Когда вы строите классификационную модель, такую как дерево решений, и хотите определить, будут ли акции расти в цене или падать на основе входных данных. Модель сначала рассчитает вероятность увеличения или уменьшения, используя предоставленные вами исторические данные. После этого, основываясь на пороговом значении, она решит, будет ли результат увеличиваться или уменьшаться.

Да, ключевое слово здесь — порог. Разные пороговые значения создают разные TPR и FPR. Они представляют те самые точки, что образуют кривую ROC. Вы можете выбрать «Увеличение» в качестве предсказания модели, если полученная на основе исторических данных вероятность роста акций больше 50%. Также можете изменить пороговое значение и отобразить «Увеличение», только если соответствующая вероятность больше 90%. Если вы установите 90% порог вместо 50%, вы будете более уверены в том, что выбранные для «Увеличения» акции действительно вырастут. Но так вы можете упустить некоторые потенциально выгодные варианты.

Что значит синяя пунктирная линия на графике?

Как мы знаем, чем больше площадь под кривой (AUC), тем лучше классификация. Идеальная или наилучшая кривая — это вертикальная линия от (0,0) до (0,1), которая тянется до (1,1). Это означает: модель всегда может различить положительные и отрицательные случаи. Однако, если вы выбираете класс случайным образом для каждого семпла, TPR и FPR должны увеличиваться с одинаковой скоростью. Синяя пунктирная линия показывает кривую TPR и FPR при случайном определении positive или negative для каждого случая. Для этой диагональной линии площадь под кривой (AUC) составляет 0.5.

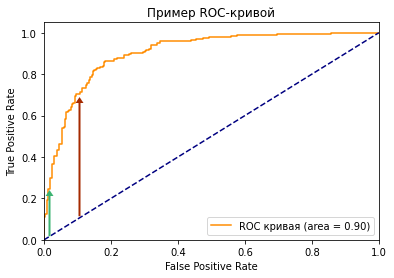
Что произойдет с TPR, FPR и ROC-кривой, если изменить пороговое значение?

Посмотрите на две точки на ROC-кривой. Зеленая точка имеет очень высокий порог, это означает, что только если вы уверены на 99%, можете классифицировать случай как positive. Красная точка имеет относительно более низкий порог. Это означает, что вы можете классифицировать случай как positive, если вы уверены на 90%.

Как изменяются TPR и FPR при движении от зеленой точки к красной?

И TPR, и FPR увеличиваются. Когда вы уменьшаете порог, модель будет определять больше положительных случаев. Таким образом, TP увеличивается, как и TP/(TP + FN). С другой стороны, вы неизбежно ошибочно классифицируете некоторые отрицательные случаи как положительные из-за снижения порога, и поэтому FP и FP/(FP + TN) также увеличиваются.

Мы видим, что TPR и FPR положительно коррелируют. Вам нужно балансировать между максимальным охватом positive случаев и минимизацией неправильной классификации negative случаев.

Как выбрать оптимальную точку на кривой ROC?

Трудно определить оптимальную точку, потому что нужно выбрать наиболее подходящее пороговое значение, учитывая сферу применения модели. Однако общее правило — максимизировать разницу (TPR-FPR), которая на графике представлена вертикальным расстоянием между оранжевой и синей пунктирной линией.

Почему площадь под кривой ROC – хорошая метрика для оценки модели классификации?

Хорошая метрика модели машинного обучения должна отображать истинную и постоянную способность модели к прогнозированию. Это означает, что, если я изменю тестовый набор данных, он не должен давать другой результат.

ROC-кривая учитывает не только результаты классификации, но и вероятность предсказания всех классов. Например, если результат корректно классифицирован на основе 51% вероятности, то он, скорее всего, будет классифицирован неверно, если вы воспользуетесь другим тестовым датасетом. Кроме того, ROC-кривая также учитывает эффективность модели при различных пороговых значениях. Она является комплексной метрикой для оценки того, насколько хорошо разделяются случаи в разных группах.

Какое значение AUC является приемлемым для модели классификации?

Как я показал ранее, для задачи двоичной классификации при определении классов случайным образом, вы можете получить 0.5 AUC. Следовательно, если вы решаете задачу бинарной классификации, разумное значение AUC должно быть > 0.5. У хорошей модели классификации показатель AUC > 0.9, но это значение сильно зависит от сферы ее применения.

Как рассчитать AUC и построить ROC-кривую в Python?

Если вы просто хотите рассчитать AUC, вы можете воспользоваться пакетом metrics библиотеки sklearn (ссылка).
Если вы хотите построить ROC-кривую для результатов вашей модели, вам стоит перейти сюда.

Вот код для построения графика ROC, который я использовал в этой статье.

Источник

Упрощение метрик ROC и AUC.

Дата публикации Mar 3, 2019

«Определение гениальности — это сложность и упрощение». — Альберт Эйнштейн

Кривые ROC и AUC являются важными метриками оценки для расчета производительности любой модели классификации. Эти определения и жаргоны довольно распространены в сообществе машинного обучения и встречаются каждым из нас, когда мы начинаем изучать модели классификации. Однако в большинстве случаев они не полностью поняты или, скорее, неправильно поняты, и их истинная сущность не может быть использована. Под капотом это очень простые параметры расчета, которые просто нужно немного демистифицировать.

Концепция ROC и AUC основывается на знании матрицы смешения, специфичности и чувствительности. Кроме того, пример, который я буду использовать в этой статье, основан на алгоритме логистической регрессии, однако важно помнить, что концепция ROC и AUC может применяться не только к логистической регрессии.

Рассмотримгипотетический примерсодержащий группу людей. Ось Y имеет две категории, т.е. Has Heart Disease представлены красными людьми и does not have Heart Disease представлены зелеными кружками. длинная ось х, мы имеемхолестеринуровни и классификатор пытается классифицировать людей на две категории в зависимости от их уровня холестерина.

На что обратить внимание:

• У окруженного Зеленого человека высокий уровень холестерина, но у него нет болезней сердца. Это может быть связано с тем, что сейчас человек ведет лучший образ жизни и регулярно занимается спортом.
• У кружившего красного человека низкий уровень холестерина все еще был сердечный приступ. Это может быть связано с тем, что у него есть другие проблемы с сердцем.

Это гипотетический пример, поэтому причины также являются гипотетическими😃

Логистическая регрессия

Теперь, если мы подгоним кривую логистической регрессии к данным, ось Y будет преобразована вВероятностьчеловека, имеющего заболевание сердца на основе уровня холестерина.

Белая точка обозначает человека, имеющего более низкую вероятность сердечных заболеваний, чем человек, представленный черной точкой.

Однако, если мы хотим классифицировать людей по двум категориям, нам нужен способ превратить вероятности в классификации. Один из способов — установить порог в 0,5. Затем классифицируйте людей с вероятностью сердечной недостаточности> 0,5 как «имея болезнь сердцаИ классифицировать людей с вероятностью сердечного заболевания

Давайте теперь оценим эффективность этой логистической регрессии с порогом классификации, установленным на 0,5, с некоторыми новыми людьми, о которых мы уже знаем, есть ли у них сердечные заболевания или нет.

Наша модель логистической регрессии правильно классифицирует всех людей, кроме лиц 1 и 2.

• Мы знаем, что у Человека 1 есть болезнь сердца, но наша модель классифицирует это как иначе.
• Мы также знаем, что у человека 2 нет болезней сердца, но опять-таки наша модель классифицирует его неправильно.

Матрица путаницы

Давайте создадим Матрицу путаницы, чтобы суммировать классификации.

После того, как запутанная матрица заполнена, мы можем вычислитьчувствительностьиспецифичностьоценить эту логистическую регрессию на 0,5 порога.

Специфичность и чувствительность

В приведенной выше матрице путаницы давайте заменим числа тем, что они на самом деле представляют.

• Истинные Позитивы (TP):Люди, которыеимел болезнь сердцаи было также предсказано, что болезнь сердца.
• Истинные негативы (TN):Люди, которыенеиметь болезнь сердцаи были также предсказаны, чтобы не иметь сердечно-сосудистых заболеваний.
• Ложные негативы (FN):Люди, у которых болезнь сердца, но прогноз говорит, что нет.
• Ложные срабатывания (FP):Люди, которыенеиметь болезнь сердцано предсказание говорит, что они делают.

Теперь мы можем рассчитать две полезные метрики на основе матрицы путаницы:

чувствительность

Чувствительность говорит нам, какой процент людейсболезни сердца были на самом деле правильно определены.

Это оказывается: 3/3 + 1 = 0,75

Это говорит нам о том, что75%людей с болезнью сердца были правильно определены нашей моделью.

специфичность

Специфика говорит нам, какой процент людейбезболезни сердца были на самом деле правильно определены.

Это оказывается: 3/3 + 1 = 0,75

Это говорит нам об этом снова75%людейбез болезней сердцабыли правильно определены нашей моделью.

Если для нас важно правильно определить положительные стороны, то мы должны выбрать модель с более высокой чувствительностью. Однако, если правильное определение негативов является более важным, то мы должны выбрать специфичность в качестве метрики измерения.

Определение правильных порогов

Теперь давайте поговорим о том, что происходит, когда мы используем другой порог для принятия решения о том, есть ли у человека болезнь сердца или нет.

• Установка порога на 0 1

Это будет правильно идентифицировать всех людей, которые имеют заболевания сердца. Человек с меткой 1 также правильно классифицирован как пациент с сердечным заболеванием.

Тем не менее, это также увеличит количество ложных срабатываний, поскольку теперь лица 2 и 3 будут ошибочно классифицированы как имеющие сердечные заболевания.

Поэтому нижний порог:

• Увеличивает количество ложных срабатываний
• Уменьшает количество ложных негативов.

Пересчет матрицы путаницы:

В этом случае становится важным правильно идентифицировать людей, страдающих сердечно-сосудистыми заболеваниями, чтобы можно было предпринять корректирующие меры, иначе болезнь сердца может привести к серьезным осложнениям. Это означает, что снижение порога — хорошая идея, даже если это приводит к большему количеству ложных положительных случаев.

• Установка порога на 0,9

Теперь это правильно идентифицирует всех людей, у которых нет болезней сердца. Однако лицо, помеченное как лицо 1, будет неправильно классифицировано как не имеющее заболевания сердца.

Поэтому нижний порог:

• Уменьшает количество ложных срабатываний
• Увеличивает количество ложных негативов.

Пересчет матрицы путаницы:

Пороговое значение может быть установлено на любое значение от 0 до 1. Итак, как мы можем определить, какой порог является лучшим? Нужно ли экспериментировать со всеми пороговыми значениями? Каждый порог приводит к разной матрице путаницы, а количество порогов приводит к большому количеству матриц путаницы, что является не лучшим способом работы.

ROC Графики

ROC (Кривая характеристики оператора приемника) может помочь в определении наилучшего порогового значения. Он генерируется путем построения истинной положительной ставки (ось Y) и ложной положительной ставки (ось X).

Истинный положительный показатель показывает, какая доля людей ‘с сердечными заболеваниямиe ‘были правильно классифицированы.

Неверно положительный показатель указывает на долю людей, классифицированных как ‘не имея болезни сердца’, Это ложные срабатывания.

Чтобы лучше узнать РПЦ, давайте начнем с нуля.

• Порог, классифицирующий всех людей как имеющих болезнь сердца.

Матрица путаницы будет:

Это означает, что истинный положительный показатель, когда порог настолько низок, что каждый отдельный человек классифицируется как имеющий сердечную болезнь, равен 1. Это означает, что каждый отдельный человек с сердечной болезнью был правильно классифицирован.

Кроме того, уровень ложных срабатываний, когда порог настолько низок, что каждый отдельный человек классифицируется как имеющий сердечную болезнь, также равен 1. Это означает, что каждый отдельный человек без сердечной болезни был ошибочно классифицирован.

Построение этой точки на графике РПЦ:

Любая точка на синих диагональных линиях означает, что доля правильно классифицированных образцов равна доле неправильно классифицированных образцов.

• Немного увеличьте порог, чтобы только два человека с наименьшим уровнем холестерина были ниже порога.

Матрица путаницы будет:

Построим эту точку (0.5,1) на графике ROC.

Это означает, что этот порог лучше, чем предыдущий.

• Теперь, если продолжаем увеличивать пороговые значения, и достигаем точки, где мы получаем следующую матрицу путаницы

Построим эту точку (0,0,75) на графике ROC.

Безусловно, это лучший порог, который мы получили, поскольку он не предсказывал ложных срабатываний.

• Наконец, мы выбираем порог, в котором мы классифицируем всех людей как не имеющих заболевания сердца, т.е. порог 1.

График, в этом случае, будет в (0,0):

Затем мы можем соединить точки, что дает нам ROC-график. График ROC суммирует матрицы путаницы, созданные для каждого порога, без необходимости их фактического расчета.

Просто взглянув на график, мы можем сделать вывод, что порог C лучше, чем порог B, и в зависимости от того, сколько ложных срабатываний мы готовы принять, мы можем выбрать оптимальный порог.

AUC обозначаетПлощадь под кривой, AUC дает показатель успешной классификации по логистической модели. AUC позволяет легко сравнить кривую ROC одной модели с другой.

ППКдля красногоРПЦкривая больше, чемППКдля голубыхROС кривой. Это означает, что красная кривая лучше. Если бы красная ROC-кривая была сгенерирована, скажем, Случайным лесом и Blue ROC с помощью Логистической регрессии, мы могли бы заключить, что классификатор Random лучше справился с классификацией пациентов.

Вывод

AUC и ROC являются важными показателями оценки для расчета эффективности работы любой модели классификации. Поэтому знакомство с тем, как они рассчитываются, так же важно, как и их использование. Надеемся, что в следующий раз, когда вы столкнетесь с этими терминами, вы сможете легко объяснить их в контексте вашей проблемы.

Источник